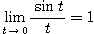 임을 증명
임을 증명
절대값이 작은 t 에 대하여 sin t = t 라는 명제는
sin x 함수를 미분하면 cos x 함수가 된다는 것의 특별한 경우입니다.
다시 말하면 원점 x = 0 에서 sin 함수의 변화율을 구하면 cos 0 = 1 이라는 말입니다
(*) 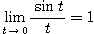 .
.
위 식을 달리 쓰면 "|t| 가 아주 작으면 sin t ≒ t 이다"입니다.
이제 등식 (*)를 증명하여 봅시다. 우선 중심각이 t 인 부채꼴 AOB를 생각합시다.
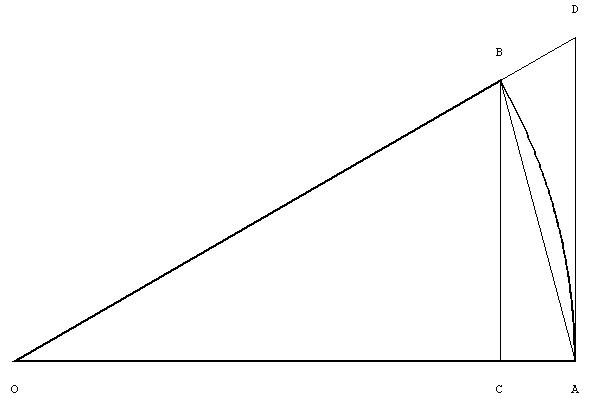
편의상 OA를 단위길이로 정하면, 호 AB 의 길이가 바로 t입니다.
그리고 점 A에서 OA 에 수직인 직선이 OB 의 연장선과 만나는 점을 D 라 하면
AD = tan t
한편 부채꼴 AOB의 넓이는 삼각형 AOB 보다 크고 삼각형 OAD 보다 작으므로,
다음 부등식을 얻습니다
sin t < t < tan t (t > 0)
이 식을 변형하면 (tan t = sin t / cos t 이므로)
(**) 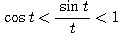
이 식은 t 가 음수라도 성립한다는 것을 바로 알 수 있을 것입니다.
그러므로 t 의 절대값이 아주 작으면 cos t 는 1 에 아주 가까워지고
따라서 sin t 와 t 의 비도 1 에 가까워집니다.
그러므로 (*) 의 증명을 마칩니다.
만약 t 와 sin t 의 비를 보는 것 대신 그들의 차를 보고 싶으면 (**)를 변형하여 정리하면
(***) | t - sin t | < |t| ( 1- cos t)
특히 |t - sin t| < |t| 임을 알지요.
서울대학교 수리과학부 Q&A 에서 발췌